Van oudsher wordt dit getal, de ‘gulden snede’ of Phi (φ) beschouwd als iets dat de ultieme verhouding van perfectie, harmonie en goddelijkheid weergeeft. Kan schoonheid berekend worden of ligt de charme van schoonheid juist in het onvoorspelbare, het onberekenbare? Door de geschiedenis heen heeft de Gulden Snede veel nieuwsgierigheid opgeroepen en terecht want we komen het getal tegen in zowel kunst, design als de natuur en allerlei andere onderdelen van het leven.
Gulden Snede
Phi (φ) is ongeveer gelijk aan 1,61803398875. Het is bekend onder namen als de ‘Gulden Snede’, gouden verdeling’ (sectio aurea), ‘gulden regel’ (ratio aurea) of ‘goddelijke verhouding’ (proportio divina).
Er wordt van dit verhoudingsgetal beweerd dat het een gevoel van balans, harmonie en natuurlijke schoonheid in design oproept bij de toeschouwer. Op de een of andere manier heeft de mensheid de ‘goddelijke verhouding’ zowel bewust als onbewust toegepast.
Door de eeuwen heen heeft het de Grieken gefascineerd, mensen tijdens de Renaissance, een 17e eeuwse sterrenkundige en 21e eeuwse romanschrijvers.
Het is beschreven door Euclides in ‘Elementen’ circa 300 B.C., door Luca Pacioli, een tijdgenoot van Leonardo Da Vinci, in ‘De Divina Proportione‘ in 1509,
door Johannes Kepler rond 1600 en door Dan Brown in 2003 in zijn roman novel ‘De Da Vinci Code’.
Het is zeker dat Leonardo da Vinci op de hoogte is geweest van de Gulden Snede, doordat hij de illustraties heeft verzorgd in het boek van Luca Pacioli.
Ik zal de lezer niet vermoeien met wiskundige bespiegelingen, het meest elementaire van phi is dat het een verhoudingsgetal is. Als je een rechthoek neemt dan is de lange zijde gelijk aan 1,618 (Phi) vermenigvuldigd met de korte zijde. Op deze manier krijg je een ‘gulden rechthoek’.
In credit cards is de gulden driehoek, de gulden verhouding toegepast.
Dat kan je zelf controleren als volgt:

Als de diagonale lijn de hoek A raakt, dan hebben deze visitekaartjes (foto) de juiste verhouding van de gulden snede. Dit hebben ze in tegenstelling tot credit cards dus niet.
Hoe vind je Phi of de Gulden Snede? (voor de liefhebbers)
Deze deelt een lijn of lengte zodanig in twee ongelijke delen, zodat de verhouding van het kleine tot het grote deel dezelfde is als die van het grote deel tot het geheel. De rechthoek met zijden a en b, die overblijft na verwijdering van het vierkant met zijde a, is gelijkvormig met de oorspronkelijke rechthoek.
Op het punt waar:
de verhouding van de lengte van een volledige lijn A
tot de lengte van het langere lijn B
GELIJK IS AAN
de verhouding van de lengte van de langere lijn B
tot de lengte van de kleinere lijn C
Zien we dat:
A is 1,618 … keer B en B is 1,618 … keer C. of
C is 0,618… van B en B is 0,618… van A.
Geschiedenis van de gulden snede
Van de Grieken wordt aangenomen dat zij het ontwerp van het Parthenon op de verhouding van de gulden snede hebben gebaseerd, maar dit wordt betwist. In ieder geval bestudeert Phidias (500 BC – 432 BC), een Griekse beeldhouwer en wiskundige, phi en past het toe op het ontwerp van het Parthenon.
Euclides (365 BC – 300 BC) verwijst in het populaire boek ‘Elementen’ al naar de Gulden Snede:
“Een rechte lijn is verdeeld in uiterste en middelste reden als de verhouding tussen de gehele lijn en het grotere deel gelijk is aan die tussen het grotere en het kleinere deel.” Dit is dus later bekend geworden als Phi, omdat het is gekoppeld aan de naam van Phidias, de bouwer van het Parthenon.
Leonardo Da Vinci voorziet het boek van Luca Pacioli in 1509 getiteld “De Divina Proportione” van illustraties. Pacioli introduceert daarmee de Gulden Snede in ideeën over schoonheid en kunst. Het boek bevat ook de beroemde tekening van Leonardo da Vinci, van de Vitruviusman, die is gebaseerd op Phi.
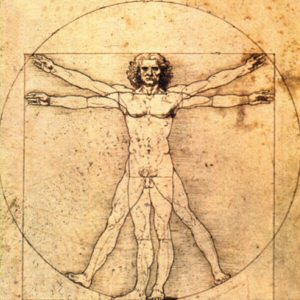
Leonardo Da Vinci gebruikt de Gulden Snede voor alle essentiële verhoudingen van zijn schilderij ‘Het Laatste Avondmaal’. De Vitruviusman of ‘ideale man’ laat de ideale verhoudingen zien van het menselijk lichaam. De verhouding tussen de zijden van het vierkant (zie foto) en de straal van de cirkel is gelijk aan de Gulden Snede. Namelijk:
Totale lengte = spanwijdte van de armen = 8 handpalmen = 6 voeten = 8 gezichten =
1,618 keer de hoogte van de navel
De term Gulden Snede is voor het eerst gebruikt als ‘Goldener Schnitt’ door Martin Ohm (1792–1872) in 1815 in zijn boek “Die reine Elementar-Mathematik“.
Pas in de twintigste eeuw wordt de term phi (Φ) gebruikt door de Amerikaanse wiskundige Mark Barr.
Phi in de Kunst
Het gebruik van de Gulden Snede wordt door verschillende kunstenaars toen en nu gebruikt.
Enkele voorbeelden zijn Michelangelo in ‘De schepping van Adam’ in de Sixtijnse kapel. Salvador Dali in zijn ‘Het sacrament van het laatste avondmaal’, Le Corbusier in zijn architectuur, Frank Lloyd Wright als inspiratie voor het ontwerp de hellingbaan van het Guggenheim Museum in New York en de Nederlandse kunstenaar Escher in een groot deel van zijn schilderijen.
De grafisch kunstenaar M.C. Escher (1898-1972) heeft jarenlang (vanaf 1941) in de gemeente Baarn gewoond en gewerkt. Eschers werk kenmerkt zich door een wiskundige perfectie. Bekend zijn de werkstukken waarbij hij in de tweede dimensie het perspectief de toeschouwer confronteert met een ‘bedrieglijk realisme’. Daarnaast kennen wij ook zijn patronen waarbij figuren tegen elkaar liggen en beesten in elkaar verwerkt zijn, om zo samen een passende eenheid te vormen.
Zijn werk speelt zich af binnen de ‘lijnen van het wiskundige’ en de daarbij horende ‘grenzen van de wetmatigheid’. Hij maakt daarom veel gebruik van driehoeken, vierkanten en zeshoeken. Deze figuren hebben een uitgebalanceerde verhouding en worden volgens principes van Gulden Snede berekend.
Rob Vellekoop, 11 augustus 2018



Comments are closed